Assume that you’ve taken a spectrum of a star, and you’d like to estimate the star’s size. Can you do it? Yes, if you also have a parallax angle for the star.

This post quickly ties together different concepts to explain how observations (spectrum and parallax) can be used to estimate the size of a star. I then introduce, and mostly gloss over, some of the messier details, because this is for an introductory astronomy course.

This post assumes that you’ve read Stellar Radii and the Stefan-Boltzmann Law and that you are familiar with…

• Wien’s law
• Parallax
• The inverse square law for light
• Stellar classification

We’ll start with a list of things that we know so far about light and stars.

• If we can find the temperature and luminosity of a star, then we can use the Stefan-Boltzmann Law to estimate the star’s size (surface area and radius).
• We can use Wien’s law to determine the temperature of a blackbody by measuring the wavelength at which the spectrum peaks.
• Let’s assume that the light we collect as a spectrum can tell us about its brightness.
• If we have a parallax angle for the star, we can calculate the distance to the star.
• If we know the brightness of a star and the distance to the star, we can use the inverse square law of light to determine its luminosity.
• Stars can be classified (OBAFGKM) using their spectra.

Putting this all together, we have a series of steps to apply to find the star’s radius…

1. Determine the temperature of the star from its spectrum.
2. Determine the brightness of the star from its spectrum.
3. Determine the distance to the star using its parallax.

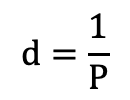
4. Determine the luminosity of the star using its brightness and the distance to the star.

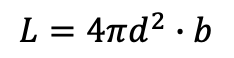
5. Determine the star’s size using its luminosity and temperature

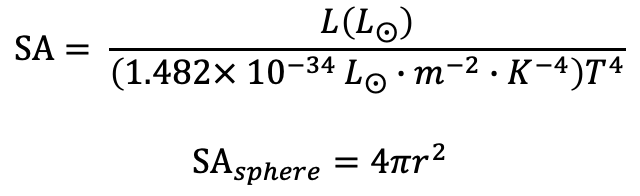
In the formulas above

• P is the parallax angle
• d is the distance to the star
• L is luminosity (the total light leaving the star)
• b is brightness (the light passing through each square meter of a telescope pointed at the star)
• SA is the star’s surface area
• T is the temperature of the star’s surface
• r is the star’s radius

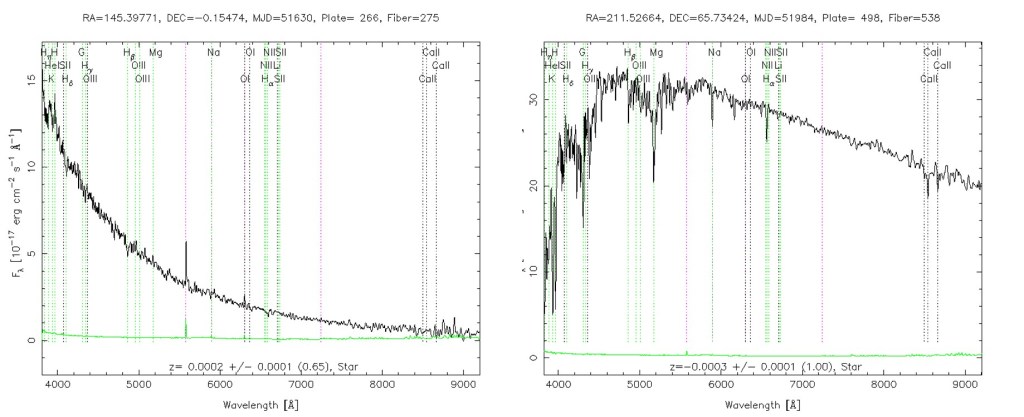
Unfortunately, looking at a couple of real stellar spectra, I anticipate a few problems…

• Are these really blackbody spectra? What about all those lines?
• Can I use Wien’s Law to find the temperature of these stars? I can’t see a peak for the spectrum on the left and the peak for the spectrum on the right is lost in all those… lines.
• What about all the light from the star that I’m missing? Clearly these spectra continue into the infrared and the ultraviolet.

These are the messier details that I promised to gloss over. Yes, astronomers can measure the temperature of a star from its spectrum. As you learned when classifying stellar spectra, the absorption lines in a spectrum can help us classify the star. The presence and strength of the lines, along with the shape of the continuum, help astronomers determine the star’s temperature. (It isn’t quite as simple as finding the spectrum’s peak.)

And the light that’s missing? A star’s classification helps us there too. Many stars have been observed across a wide range of wavelengths. We assume that the parts of the spectrum that we haven’t observed are similar to the spectra for other stars of the same type (O, B, G, etc.). With this assumption, we estimate how much light we’re missing. The result is a bolometric luminosity, or a luminosity that includes all of the light from a star (across all wavelengths). This is opposed to, for example, the visible luminosity of a star, which would include only light in visible wavelengths. It’s the bolometric luminosity, along with the temperature, that we use in the Stefan-Boltzmann law to estimate the star’s size.

Entries in this Series (Stellar Properties)

Magnitude and Parallax

• Bright Stars – Luminous or Nearby
• A Brief Introduction to the Magnitude System
• Apparent and Absolute Magnitude
• Parallax

Luminosity and Size

• Measuring a Star’s Size – The Challenge
• Stellar Radii and the Stefan-Boltzmann Law
• Stellar Radii and Stellar Spectra