You can estimate a star’s size if you know its temperature and luminosity. To do this, assume that the surface of the star is a giant blackbody, then apply the Stefan-Boltzmann Law.

The Stefan-Boltzmann law is discussed in section 5.2 of OpenStax Astronomy. To summarize, it states that the luminosity (total energy output as light) of a blackbody increases when the object gets hotter or larger. This makes sense because the hotter an object is the more internal energy it has to radiate away, and a blackbody radiates across its entire surface area.

Placing the Stefan-Boltzmann law in context…

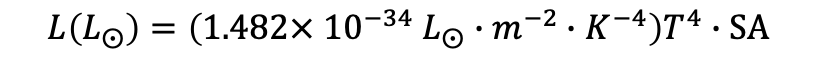
Where L is the star’s luminosity in multiples of the Sun’s luminosity, T is the star’s surface temperature in Kelvin, and SA is the surface area of the star in square meters.

If you Google Stefan-Boltzmann Law, you’ll find a slightly different equation. I’ve converted from Watts to solar luminosity (a good unit for stars) and multiplied by surface area so that the equation results in luminosity instead of flux per square meter. The basic physical equation is the same; this is just the law “in context”.

If you look at the law, you can see a power of 4 hanging out above the T (temperature). This power of 4 means that the radiant flux (luminosity per square meter) from a blackbody is extremely dependent on temperature. If the temperature doubles (say from 3,000 K to 6,000 K), then the radiant flux will increase not by a factor of 2, or even a factor of 4, but by an impressive factor of 16.

This power of 4 in the Stefan-Boltzman law is how Sirius can be 25 times brighter than the Sun with a radius that is only 1.7 times as large. Sirius is bluer than the Sun, indicating that it is hotter, and more radiant.

If you know the temperature and luminosity of a star, then to estimate its size you rearrange the above equation, plug in L and T, and solve. If you want to find the radius instead of the surface area, use geometry.

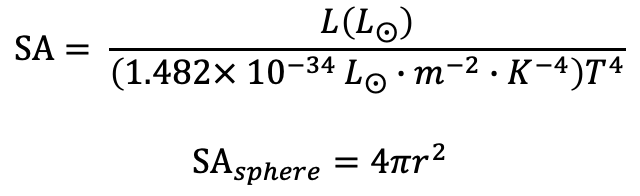
Entries in this Series (Stellar Properties)

Magnitude and Parallax

• Bright Stars – Luminous or Nearby
• A Brief Introduction to the Magnitude System
• Apparent and Absolute Magnitude
• Parallax

Luminosity and Size

• Measuring a Star’s Size – The Challenge
• Stellar Radii and the Stefan-Boltzmann Law
• Stellar Radii and Stellar Spectra