Warning: Math Ahead. Don’t Panic.

Our goal is to find the luminosity of and distance to a star. We know we can’t find both, or even either, of these properties by observing only the brightness of a star. We also know that the problem is that stars come in a wide range of luminosity and vary greatly in their distances from the Sun. What appears to be a bright star might be very close (Rigil Kentaurus A) or intrinsically very luminous (Rigel) or a little bit of both (Sirius).

In the magnitude system, we approach this problem by talking about apparent magnitude and absolute magnitude. The apparent in apparent magnitude is “what you see”, what is apparent. Apparent magnitude is what we measure with our telescope/camera. The absolute in absolute magnitude implies something that is fixed and unchanging. If we could board an interstellar spaceship and travel through the stars, their apparent magnitudes would change – getting brighter as they got closer and dimmer as they got farther away. Their absolute magnitudes would not.

If we don’t know how far away a star is, then we can’t figure out its absolute magnitude, we can only measure its apparent magnitude. But if we can figure out how far away a star is, then we can calculate its absolute magnitude.

The basic principle behind this is the inverse square law of light. After much YouTube searching, the video I found that did the best job of succinctly explaining the inverse square law was the following video on its application to photography and cinematography. Watch the first four minutes of the video to see the explanation.

To reiterate, the inverse in the inverse square law means that as a star gets further away, it gets dimmer. Increasing distance means decreasing brightness. The square in the inverse square law means that this drop off happens as the square of the distance. If you double the distance, brightness doesn’t just halve, it quarters. (If you halve the distance, brightness doesn’t double, it quadruples.)

The inverse square law works fairly well with the magnitude system. Imagine two stars with equal luminosity (equal absolute magnitudes), one of which is twice as far away. The further star…

• Is dimmer
• Has a higher apparent magnitude
• Has a brightness that is a quarter that of the closer star
• Has an apparent magnitude that is about 1.5 larger than the closer star

If the closer star has an apparent magnitude of 10, the further star has an apparent magnitude of about 11.5. Easy peasy.

The magnitude system is set up to work perfectly when you multiply the distance by 10. Ten squared (10*10) is 100. So a star that is 10 times further away is 100 times fainter. If a star is 100 times fainter, its apparent magnitude increases by exactly 5.

For example if star A is 10 parsecs (a measure of distance) away and has an apparent magnitude of 12, then an equally luminous star 100 parsecs away would have an apparent magnitude of 17, and an equally luminous star 1000 parsecs away would have an apparent magnitude of 22. Every time the distance increases by a factor of 10 (is multiplied by 10), the apparent magnitude increases by 5.

Unfortunately, we don’t get to stop there. Comparing apparent magnitudes can be useful, but we want to use the inverse square law to find the absolute magnitude. To do this, we need a better definition of absolute magnitude. So…

Absolute magnitude is the (apparent) magnitude that a star would have if it were exactly 10 parsecs (a measure of distance) away.

So in the example above, the absolute magnitude of the three identical stars would be 12 (the apparent magnitude of the star that was 10 parsecs away).

When we put this into an equation, a logarithm gets involved. We’re going to take the log₁₀ (log base 10) of the distance to the star. This simply tells us how many factors of ten away the star is. If the star is 10 parsecs away, the log₁₀ of the distance is 1 (one power of 10). If the star is 100 parsecs away, the log₁₀ of the distance is 2 (two powers of 10). And if the star is 10,000 parsecs away, the log₁₀ of the distance is 5 (five powers of 10, or 10*10*10*10*10).

The equation to find the apparent magnitude if you know the absolute magnitude and the distance (in parsecs) is…

In this equation, m is the apparent magnitude, M is the absolute magnitude, and d is the distance in parsecs. You can see the 5 corresponding to 100 times fainter, and the log₁₀ of the distance. The plus sign after M lets you know that apparent magnitude (m) is going to increase as the distance gets larger.

The equation to find the absolute magnitude if you know the apparent magnitude and the distance is…

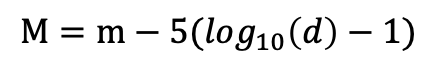
Now there’s a negative sign between m and the log term. If you have two stars with equal brightness (equal m), the star that is further away has a higher luminosity. Which means, because magnitude is strange, that is has a smaller absolute magnitude (M) and hence the negative sign.

If you’re with me this far, and you want to know what that -1 is doing hanging out in the parentheses, then let’s return to our example star with a magnitude of 12 that is 10 parsecs away. Talking through the math…

The log₁₀ of ten is one, one minus one is zero, 5 times zero is zero, so M equals m.

And absolute magnitude (M) should equal apparent magnitude (m) for this star, because it is 10 parsecs away. The -1 takes care of the fact that absolute magnitude is defined using a distance of 10 parsecs (not zero parsecs).

Entries in this Series (Stellar Properties)

Magnitude and Parallax

• Bright Stars – Luminous or Nearby
• A Brief Introduction to the Magnitude System
• Apparent and Absolute Magnitude
• Parallax

Luminosity and Size

• Measuring a Star’s Size – The Challenge
• Stellar Radii and the Stefan-Boltzmann Law
• Stellar Radii and Stellar Spectra